numpy.random.RandomState.weibull¶

RandomState.weibull(a, size=None)¶

Draw samples from a Weibull distribution.

Draw samples from a 1-parameter Weibull distribution with the given shape parameter a.

$X = (-ln(U))^{1/a}$

Here, U is drawn from the uniform distribution over (0,1].

The more common 2-parameter Weibull, including a scale parameter $\lambda$ is just $X = \lambda(-ln(U))^{1/a}$ .

Parameters:	a : float or array_like of floats Shape of the distribution. Should be greater than zero. size : int or tuple of ints, optional Output shape. If the given shape is, e.g., `(m, n, k)`, then `m * n * k` samples are drawn. If size is `None` (default), a single value is returned if `a` is a scalar. Otherwise, `np.array(a).size` samples are drawn.
Returns:	out : ndarray or scalar Drawn samples from the parameterized Weibull distribution.

Notes

The Weibull (or Type III asymptotic extreme value distribution for smallest values, SEV Type III, or Rosin-Rammler distribution) is one of a class of Generalized Extreme Value (GEV) distributions used in modeling extreme value problems. This class includes the Gumbel and Frechet distributions.

The probability density for the Weibull distribution is

$p(x) = \frac{a} {\lambda}(\frac{x}{\lambda})^{a-1}e^{-(x/\lambda)^a},$

where $a$ is the shape and $\lambda$ the scale.

The function has its peak (the mode) at $\lambda(\frac{a-1}{a})^{1/a}$ .

When a = 1, the Weibull distribution reduces to the exponential distribution.

References

[1]	Waloddi Weibull, Royal Technical University, Stockholm, 1939 “A Statistical Theory Of The Strength Of Materials”, Ingeniorsvetenskapsakademiens Handlingar Nr 151, 1939, Generalstabens Litografiska Anstalts Forlag, Stockholm.

[2]	Waloddi Weibull, “A Statistical Distribution Function of Wide Applicability”, Journal Of Applied Mechanics ASME Paper 1951.

[3]	Wikipedia, “Weibull distribution”, http://en.wikipedia.org/wiki/Weibull_distribution

Examples

Draw samples from the distribution:

>>> a = 5. # shape
>>> s = np.random.weibull(a, 1000)

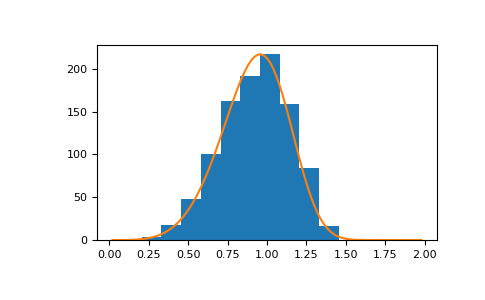
Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> x = np.arange(1,100.)/50.
>>> def weib(x,n,a):
...     return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)

>>> count, bins, ignored = plt.hist(np.random.weibull(5.,1000))
>>> x = np.arange(1,100.)/50.
>>> scale = count.max()/weib(x, 1., 5.).max()
>>> plt.plot(x, weib(x, 1., 5.)*scale)
>>> plt.show()

../../_images/numpy-random-RandomState-weibull-1.png

Previous topic

Next topic

Quick search

numpy.random.RandomState.weibull¶