numpy.absolute

numpy.absolute(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) = <ufunc 'absolute'>

Calculate the absolute value element-wise.

np.abs is a shorthand for this function.

Parameters:

xarray_like

Input array.

outndarray, None, or tuple of ndarray and None, optional

A location into which the result is stored. If provided, it must have a shape that the inputs broadcast to. If not provided or None, a freshly-allocated array is returned. A tuple (possible only as a keyword argument) must have length equal to the number of outputs.

wherearray_like, optional

This condition is broadcast over the input. At locations where the condition is True, the out array will be set to the ufunc result. Elsewhere, the out array will retain its original value. Note that if an uninitialized out array is created via the default out=None, locations within it where the condition is False will remain uninitialized.

**kwargs

For other keyword-only arguments, see the ufunc docs.

Returns:

absolutendarray

An ndarray containing the absolute value of each element in x. For complex input, a + ib, the absolute value is \(\sqrt{ a^2 + b^2 }\). This is a scalar if x is a scalar.

Examples

>>> x = np.array([-1.2, 1.2])
>>> np.absolute(x)
array([ 1.2,  1.2])
>>> np.absolute(1.2 + 1j)
1.5620499351813308

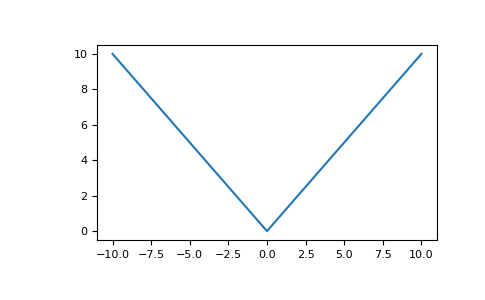
Plot the function over [-10, 10]:

>>> import matplotlib.pyplot as plt

>>> x = np.linspace(start=-10, stop=10, num=101)
>>> plt.plot(x, np.absolute(x))
>>> plt.show()

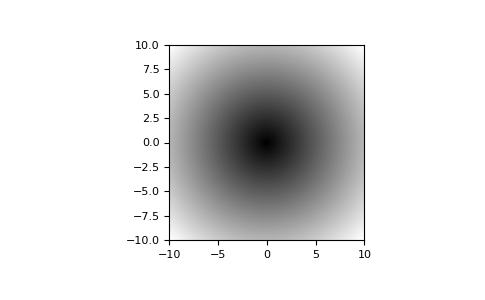
Plot the function over the complex plane:

>>> xx = x + 1j * x[:, np.newaxis]
>>> plt.imshow(np.abs(xx), extent=[-10, 10, -10, 10], cmap='gray')
>>> plt.show()

The abs function can be used as a shorthand for np.absolute on ndarrays.

>>> x = np.array([-1.2, 1.2])
>>> abs(x)
array([1.2, 1.2])