numpy.fft.fft#

fft.fft(a, n=None, axis=-1, norm=None)[source]#

Compute the one-dimensional discrete Fourier Transform.

This function computes the one-dimensional n-point discrete Fourier Transform (DFT) with the efficient Fast Fourier Transform (FFT) algorithm [CT].

Parameters:

aarray_like: Input array, can be complex.
nint, optional: Length of the transformed axis of the output. If n is smaller than the length of the input, the input is cropped. If it is larger, the input is padded with zeros. If n is not given, the length of the input along the axis specified by axis is used.
axisint, optional: Axis over which to compute the FFT. If not given, the last axis is used.
norm{“backward”, “ortho”, “forward”}, optional: New in version 1.10.0.

Normalization mode (see numpy.fft). Default is “backward”. Indicates which direction of the forward/backward pair of transforms is scaled and with what normalization factor.

New in version 1.20.0: The “backward”, “forward” values were added.

Returns:

outcomplex ndarray: The truncated or zero-padded input, transformed along the axis indicated by axis, or the last one if axis is not specified.

Raises:

IndexError: If axis is not a valid axis of a.

See also

numpy.fft: for definition of the DFT and conventions used.
ifft: The inverse of fft.
fft2: The two-dimensional FFT.
fftn: The n-dimensional FFT.
rfftn: The n-dimensional FFT of real input.
fftfreq: Frequency bins for given FFT parameters.

Notes

FFT (Fast Fourier Transform) refers to a way the discrete Fourier Transform (DFT) can be calculated efficiently, by using symmetries in the calculated terms. The symmetry is highest when n is a power of 2, and the transform is therefore most efficient for these sizes.

The DFT is defined, with the conventions used in this implementation, in the documentation for the numpy.fft module.

References

[CT]

Cooley, James W., and John W. Tukey, 1965, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19: 297-301.

Examples

>>> np.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-2.33486982e-16+1.14423775e-17j,  8.00000000e+00-1.25557246e-15j,
        2.33486982e-16+2.33486982e-16j,  0.00000000e+00+1.22464680e-16j,
       -1.14423775e-17+2.33486982e-16j,  0.00000000e+00+5.20784380e-16j,
        1.14423775e-17+1.14423775e-17j,  0.00000000e+00+1.22464680e-16j])

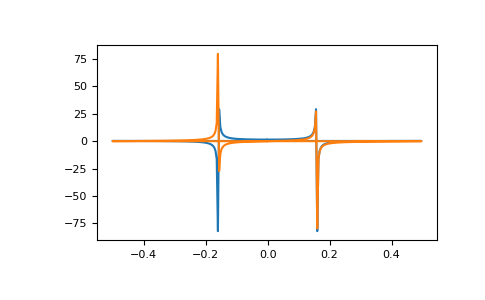
In this example, real input has an FFT which is Hermitian, i.e., symmetric in the real part and anti-symmetric in the imaginary part, as described in the numpy.fft documentation:

>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
>>> sp = np.fft.fft(np.sin(t))
>>> freq = np.fft.fftfreq(t.shape[-1])
>>> plt.plot(freq, sp.real, freq, sp.imag)
[<matplotlib.lines.Line2D object at 0x...>, <matplotlib.lines.Line2D object at 0x...>]
>>> plt.show()