Computación con Arreglos
La computación con arreglos es la base del cómputo estadístico, matemático y científico en varias aplicaciones contemporáneas de ciencia de datos y aplicaciones de analíticas, tales como la visualización de datos, el procesamiento digital de señales, el procesamiento de imágenes, la bioinformática, el aprendizaje automático, la inteligencia artificial, entre muchas otras.
La manipulación y transformación de datos a gran escala depende de una computación con arreglos eficiente y de alto rendimiento. El lenguaje de elección para la analítica de datos, el aprendizaje automático y el cómputo numérico productivo es Python.
Numerical Python o NumPy es la biblioteca estándar de-facto del lenguaje de programación Python que soporta arreglos y matrices multidimensionales de gran tamaño, y viene con una amplia colección de funciones matemáticas de alto nivel para operar sobre estos arreglos.
Tras el lanzamiento de NumPy en 2006, Pandas apareció en el panorama en 2008, y no fue hasta hace un par de años que aparecieron sucesivamente varias bibliotecas de computación con arreglos, poblando este escenario. Muchas de estas nuevas bibliotecas imitan las características y capacidades de NumPy, y contienen nuevos algoritmos y características orientadas a las aplicaciones de aprendizaje automático e inteligencia artificial.
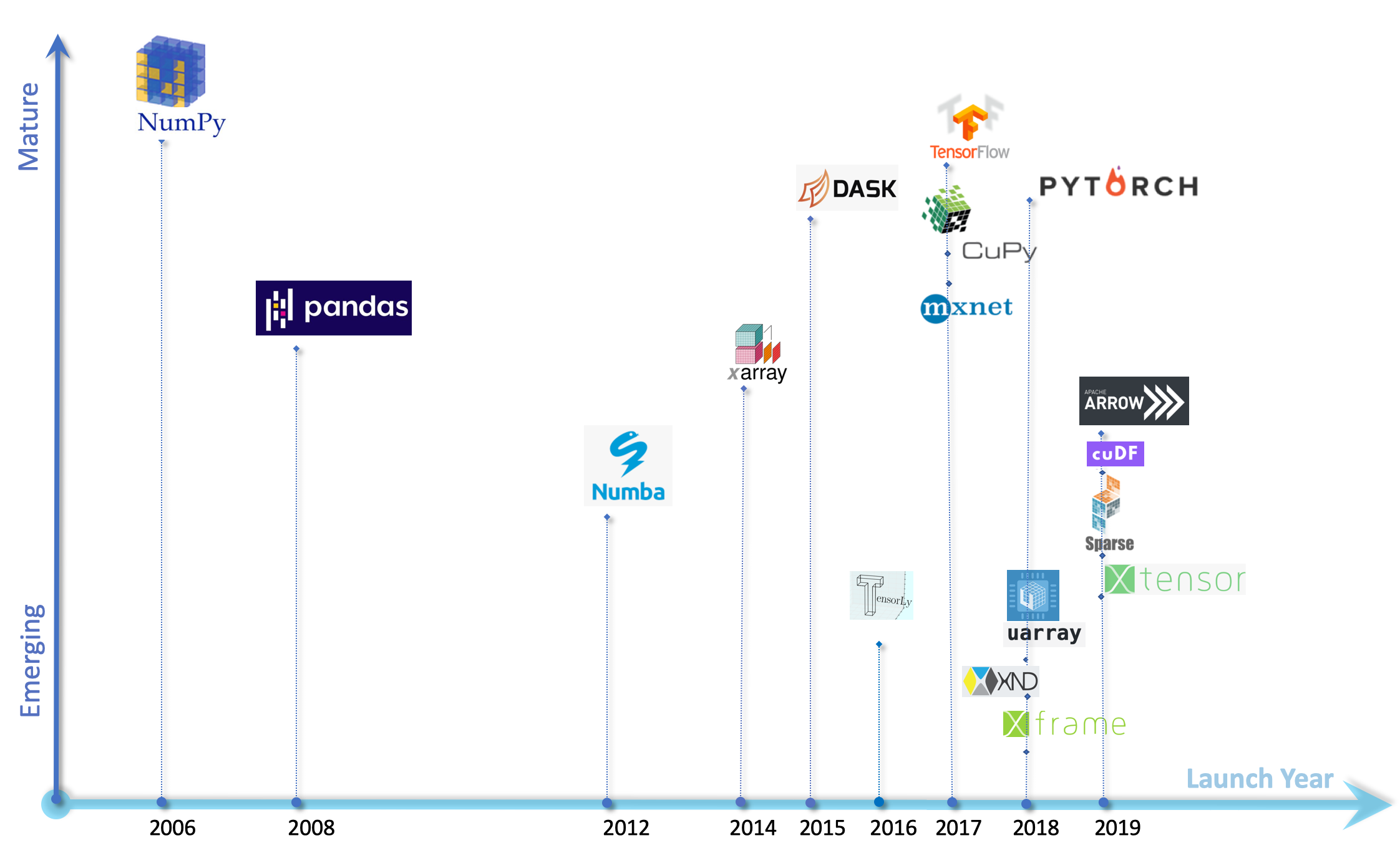
La computación con arreglos está basada en los arreglos como estructura de datos. Los arreglos son utilizados para organizar grandes cantidades de datos de manera que un conjunto de valores relacionados pueda ordenarse, buscarse, manipularse matemáticamente y transformarse con facilidad y rapidez.
La computación con arreglos es única ya que implica operar sobre todos los datos del arreglo al mismo tiempo. Esto significa que cualquier operación de arreglos se aplica a un conjunto completo de valores de una sola vez. Este enfoque vectorial proporciona velocidad y simplicidad, al permitir a los programadores codificar y operar sobre los datos agregados, sin tener que utilizar bucles de instrucciones escalares individuales.