numpy.blackman#
- numpy.blackman(M)[source]#
Return the Blackman window.
The Blackman window is a taper formed by using the first three terms of a summation of cosines. It was designed to have close to the minimal leakage possible. It is close to optimal, only slightly worse than a Kaiser window.
- Parameters:
- Mint
Number of points in the output window. If zero or less, an empty array is returned.
- Returns:
- outndarray
The window, with the maximum value normalized to one (the value one appears only if the number of samples is odd).
Notes
The Blackman window is defined as
\[w(n) = 0.42 - 0.5 \cos(2\pi n/M) + 0.08 \cos(4\pi n/M)\]Most references to the Blackman window come from the signal processing literature, where it is used as one of many windowing functions for smoothing values. It is also known as an apodization (which means “removing the foot”, i.e. smoothing discontinuities at the beginning and end of the sampled signal) or tapering function. It is known as a “near optimal” tapering function, almost as good (by some measures) as the kaiser window.
References
Blackman, R.B. and Tukey, J.W., (1958) The measurement of power spectra, Dover Publications, New York.
Oppenheim, A.V., and R.W. Schafer. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999, pp. 468-471.
Examples
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> np.blackman(12) array([-1.38777878e-17, 3.26064346e-02, 1.59903635e-01, # may vary 4.14397981e-01, 7.36045180e-01, 9.67046769e-01, 9.67046769e-01, 7.36045180e-01, 4.14397981e-01, 1.59903635e-01, 3.26064346e-02, -1.38777878e-17])
Plot the window and the frequency response.
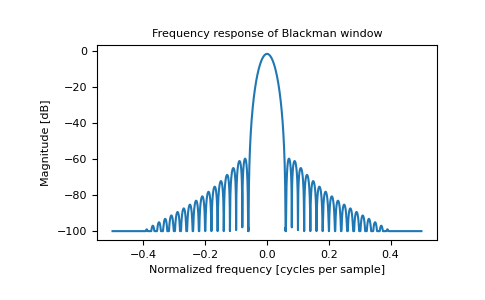
import matplotlib.pyplot as plt from numpy.fft import fft, fftshift window = np.blackman(51) plt.plot(window) plt.title("Blackman window") plt.ylabel("Amplitude") plt.xlabel("Sample") plt.show() # doctest: +SKIP
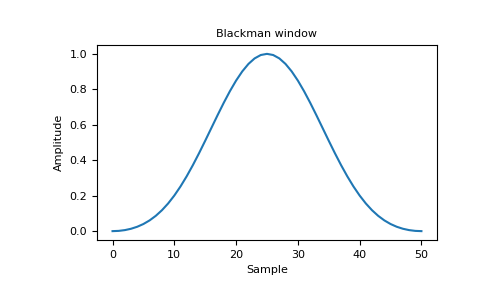
plt.figure() A = fft(window, 2048) / 25.5 mag = np.abs(fftshift(A)) freq = np.linspace(-0.5, 0.5, len(A)) with np.errstate(divide='ignore', invalid='ignore'): response = 20 * np.log10(mag) response = np.clip(response, -100, 100) plt.plot(freq, response) plt.title("Frequency response of Blackman window") plt.ylabel("Magnitude [dB]") plt.xlabel("Normalized frequency [cycles per sample]") plt.axis('tight') plt.show()