numpy.random.RandomState.poisson

method

random.RandomState.poisson(lam=1.0, size=None)

Draw samples from a Poisson distribution.

The Poisson distribution is the limit of the binomial distribution for large N.

Note

New code should use the poisson method of a Generator instance instead; please see the Quick start.

Parameters:

lamfloat or array_like of floats

Expected number of events occurring in a fixed-time interval, must be >= 0. A sequence must be broadcastable over the requested size.

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. If size is None (default), a single value is returned if lam is a scalar. Otherwise, np.array(lam).size samples are drawn.

Returns:

outndarray or scalar

Drawn samples from the parameterized Poisson distribution.

See also

random.Generator.poisson

which should be used for new code.

Notes

The probability mass function (PMF) of Poisson distribution is

\[f(k; \lambda)=\frac{\lambda^k e^{-\lambda}}{k!}\]

For events with an expected separation \(\lambda\) the Poisson distribution \(f(k; \lambda)\) describes the probability of \(k\) events occurring within the observed interval \(\lambda\).

Because the output is limited to the range of the C int64 type, a ValueError is raised when lam is within 10 sigma of the maximum representable value.

References

[1]

Weisstein, Eric W. “Poisson Distribution.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/PoissonDistribution.html

[2]

Wikipedia, “Poisson distribution”, https://en.wikipedia.org/wiki/Poisson_distribution

Examples

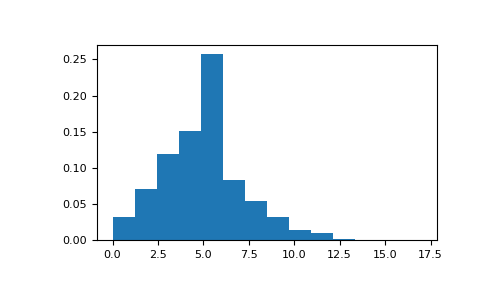
Draw samples from the distribution:

>>> import numpy as np
>>> s = np.random.poisson(5, 10000)

Display histogram of the sample:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 14, density=True)
>>> plt.show()

Draw each 100 values for lambda 100 and 500:

>>> s = np.random.poisson(lam=(100., 500.), size=(100, 2))