numpy.random.uniform

random.uniform(low=0.0, high=1.0, size=None)

Draw samples from a uniform distribution.

Samples are uniformly distributed over the half-open interval [low, high) (includes low, but excludes high). In other words, any value within the given interval is equally likely to be drawn by uniform.

Note

New code should use the uniform method of a Generator instance instead; please see the Quick start.

Parameters:

lowfloat or array_like of floats, optional

Lower boundary of the output interval. All values generated will be greater than or equal to low. The default value is 0.

highfloat or array_like of floats

Upper boundary of the output interval. All values generated will be less than or equal to high. The high limit may be included in the returned array of floats due to floating-point rounding in the equation low + (high-low) * random_sample(). The default value is 1.0.

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. If size is None (default), a single value is returned if low and high are both scalars. Otherwise, np.broadcast(low, high).size samples are drawn.

Returns:

outndarray or scalar

Drawn samples from the parameterized uniform distribution.

See also

randint

Discrete uniform distribution, yielding integers.

random_integers

Discrete uniform distribution over the closed interval [low, high].

random_sample

Floats uniformly distributed over [0, 1).

random

Alias for random_sample.

rand

Convenience function that accepts dimensions as input, e.g., rand(2,2) would generate a 2-by-2 array of floats, uniformly distributed over [0, 1).

random.Generator.uniform

which should be used for new code.

Notes

The probability density function of the uniform distribution is

\[p(x) = \frac{1}{b - a}\]

anywhere within the interval [a, b), and zero elsewhere.

When high == low, values of low will be returned. If high < low, the results are officially undefined and may eventually raise an error, i.e. do not rely on this function to behave when passed arguments satisfying that inequality condition. The high limit may be included in the returned array of floats due to floating-point rounding in the equation low + (high-low) * random_sample(). For example:

>>> x = np.float32(5*0.99999999)
>>> x
np.float32(5.0)

Examples

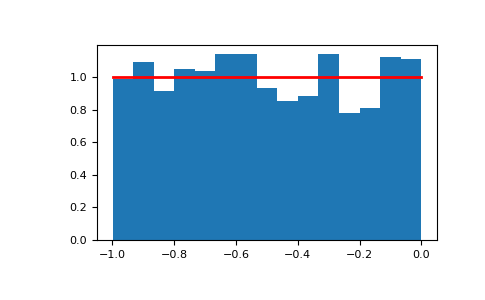
Draw samples from the distribution:

>>> s = np.random.uniform(-1,0,1000)

All values are within the given interval:

>>> np.all(s >= -1)
True
>>> np.all(s < 0)
True

Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 15, density=True)
>>> plt.plot(bins, np.ones_like(bins), linewidth=2, color='r')
>>> plt.show()