numpy.geomspace

numpy.geomspace(start, stop, num=50, endpoint=True, dtype=None, axis=0)

Return numbers spaced evenly on a log scale (a geometric progression).

This is similar to logspace, but with endpoints specified directly. Each output sample is a constant multiple of the previous.

Changed in version 1.16.0: Non-scalar start and stop are now supported.

Parameters

startarray_like

The starting value of the sequence.

stoparray_like

The final value of the sequence, unless endpoint is False. In that case, num + 1 values are spaced over the interval in log-space, of which all but the last (a sequence of length num) are returned.

numinteger, optional

Number of samples to generate. Default is 50.

endpointboolean, optional

If true, stop is the last sample. Otherwise, it is not included. Default is True.

dtypedtype

The type of the output array. If dtype is not given, infer the data type from the other input arguments.

axisint, optional

The axis in the result to store the samples. Relevant only if start or stop are array-like. By default (0), the samples will be along a new axis inserted at the beginning. Use -1 to get an axis at the end.

New in version 1.16.0.

Returns

samplesndarray

num samples, equally spaced on a log scale.

See also

logspace

Similar to geomspace, but with endpoints specified using log and base.

linspace

Similar to geomspace, but with arithmetic instead of geometric progression.

arange

Similar to linspace, with the step size specified instead of the number of samples.

Notes

If the inputs or dtype are complex, the output will follow a logarithmic spiral in the complex plane. (There are an infinite number of spirals passing through two points; the output will follow the shortest such path.)

Examples

>>> np.geomspace(1, 1000, num=4)
array([    1.,    10.,   100.,  1000.])
>>> np.geomspace(1, 1000, num=3, endpoint=False)
array([   1.,   10.,  100.])
>>> np.geomspace(1, 1000, num=4, endpoint=False)
array([   1.        ,    5.62341325,   31.6227766 ,  177.827941  ])
>>> np.geomspace(1, 256, num=9)
array([   1.,    2.,    4.,    8.,   16.,   32.,   64.,  128.,  256.])

Note that the above may not produce exact integers:

>>> np.geomspace(1, 256, num=9, dtype=int)
array([  1,   2,   4,   7,  16,  32,  63, 127, 256])
>>> np.around(np.geomspace(1, 256, num=9)).astype(int)
array([  1,   2,   4,   8,  16,  32,  64, 128, 256])

Negative, decreasing, and complex inputs are allowed:

>>> np.geomspace(1000, 1, num=4)
array([1000.,  100.,   10.,    1.])
>>> np.geomspace(-1000, -1, num=4)
array([-1000.,  -100.,   -10.,    -1.])
>>> np.geomspace(1j, 1000j, num=4)  # Straight line
array([0.   +1.j, 0.  +10.j, 0. +100.j, 0.+1000.j])
>>> np.geomspace(-1+0j, 1+0j, num=5)  # Circle
array([-1.00000000e+00+1.22464680e-16j, -7.07106781e-01+7.07106781e-01j,
        6.12323400e-17+1.00000000e+00j,  7.07106781e-01+7.07106781e-01j,
        1.00000000e+00+0.00000000e+00j])

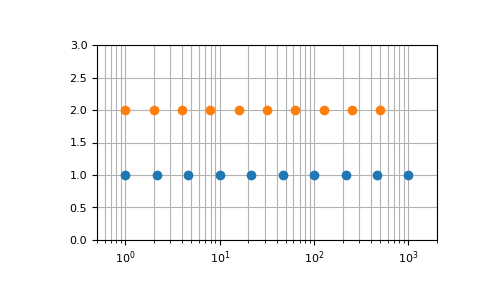
Graphical illustration of endpoint parameter:

>>> import matplotlib.pyplot as plt
>>> N = 10
>>> y = np.zeros(N)
>>> plt.semilogx(np.geomspace(1, 1000, N, endpoint=True), y + 1, 'o')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.semilogx(np.geomspace(1, 1000, N, endpoint=False), y + 2, 'o')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.axis([0.5, 2000, 0, 3])
[0.5, 2000, 0, 3]
>>> plt.grid(True, color='0.7', linestyle='-', which='both', axis='both')
>>> plt.show()