numpy.interp

numpy.interp(x, xp, fp, left=None, right=None, period=None)

One-dimensional linear interpolation for monotonically increasing sample points.

Returns the one-dimensional piecewise linear interpolant to a function with given discrete data points (xp, fp), evaluated at x.

Parameters:

xarray_like

The x-coordinates at which to evaluate the interpolated values.

xp1-D sequence of floats

The x-coordinates of the data points, must be increasing if argument period is not specified. Otherwise, xp is internally sorted after normalizing the periodic boundaries with xp = xp % period.

fp1-D sequence of float or complex

The y-coordinates of the data points, same length as xp.

leftoptional float or complex corresponding to fp

Value to return for x < xp[0], default is fp[0].

rightoptional float or complex corresponding to fp

Value to return for x > xp[-1], default is fp[-1].

periodNone or float, optional

A period for the x-coordinates. This parameter allows the proper interpolation of angular x-coordinates. Parameters left and right are ignored if period is specified.

New in version 1.10.0.

Returns:

yfloat or complex (corresponding to fp) or ndarray

The interpolated values, same shape as x.

Raises:

ValueError

If xp and fp have different length If xp or fp are not 1-D sequences If period == 0

Warning

The x-coordinate sequence is expected to be increasing, but this is not explicitly enforced. However, if the sequence xp is non-increasing, interpolation results are meaningless.

Note that, since NaN is unsortable, xp also cannot contain NaNs.

A simple check for xp being strictly increasing is:

np.all(np.diff(xp) > 0)

See also

scipy.interpolate

Examples

>>> import numpy as np
>>> xp = [1, 2, 3]
>>> fp = [3, 2, 0]
>>> np.interp(2.5, xp, fp)
1.0
>>> np.interp([0, 1, 1.5, 2.72, 3.14], xp, fp)
array([3.  , 3.  , 2.5 , 0.56, 0.  ])
>>> UNDEF = -99.0
>>> np.interp(3.14, xp, fp, right=UNDEF)
-99.0

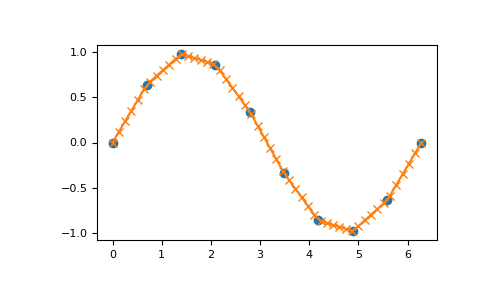
Plot an interpolant to the sine function:

>>> x = np.linspace(0, 2*np.pi, 10)
>>> y = np.sin(x)
>>> xvals = np.linspace(0, 2*np.pi, 50)
>>> yinterp = np.interp(xvals, x, y)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.plot(xvals, yinterp, '-x')
[<matplotlib.lines.Line2D object at 0x...>]
>>> plt.show()

Interpolation with periodic x-coordinates:

>>> x = [-180, -170, -185, 185, -10, -5, 0, 365]
>>> xp = [190, -190, 350, -350]
>>> fp = [5, 10, 3, 4]
>>> np.interp(x, xp, fp, period=360)
array([7.5 , 5.  , 8.75, 6.25, 3.  , 3.25, 3.5 , 3.75])

Complex interpolation:

>>> x = [1.5, 4.0]
>>> xp = [2,3,5]
>>> fp = [1.0j, 0, 2+3j]
>>> np.interp(x, xp, fp)
array([0.+1.j , 1.+1.5j])