numpy.fft.fftn#

fft.fftn(a, s=None, axes=None, norm=None, out=None)[source]#

Compute the N-dimensional discrete Fourier Transform.

This function computes the N-dimensional discrete Fourier Transform over any number of axes in an M-dimensional array by means of the Fast Fourier Transform (FFT).

Parameters:

aarray_like

Input array, can be complex.

ssequence of ints, optional

Shape (length of each transformed axis) of the output (s[0] refers to axis 0, s[1] to axis 1, etc.). This corresponds to n for fft(x, n). Along any axis, if the given shape is smaller than that of the input, the input is cropped. If it is larger, the input is padded with zeros.

Changed in version 2.0: If it is -1, the whole input is used (no padding/trimming).

If s is not given, the shape of the input along the axes specified by axes is used.

Deprecated since version 2.0: If s is not None, axes must not be None either.

Deprecated since version 2.0: s must contain only int s, not None values. None values currently mean that the default value for n is used in the corresponding 1-D transform, but this behaviour is deprecated.

axessequence of ints, optional

Axes over which to compute the FFT. If not given, the last len(s) axes are used, or all axes if s is also not specified. Repeated indices in axes means that the transform over that axis is performed multiple times.

Deprecated since version 2.0: If s is specified, the corresponding axes to be transformed must be explicitly specified too.

norm{“backward”, “ortho”, “forward”}, optional

Normalization mode (see numpy.fft). Default is “backward”. Indicates which direction of the forward/backward pair of transforms is scaled and with what normalization factor.

New in version 1.20.0: The “backward”, “forward” values were added.

outcomplex ndarray, optional

If provided, the result will be placed in this array. It should be of the appropriate shape and dtype for all axes (and hence is incompatible with passing in all but the trivial s).

New in version 2.0.0.

Returns:

outcomplex ndarray: The truncated or zero-padded input, transformed along the axes indicated by axes, or by a combination of s and a, as explained in the parameters section above.

Raises:

ValueError: If s and axes have different length.
IndexError: If an element of axes is larger than than the number of axes of a.

See also

numpy.fft: Overall view of discrete Fourier transforms, with definitions and conventions used.
ifftn: The inverse of fftn, the inverse n-dimensional FFT.
fft: The one-dimensional FFT, with definitions and conventions used.
rfftn: The n-dimensional FFT of real input.
fft2: The two-dimensional FFT.
fftshift: Shifts zero-frequency terms to centre of array

Notes

The output, analogously to fft, contains the term for zero frequency in the low-order corner of all axes, the positive frequency terms in the first half of all axes, the term for the Nyquist frequency in the middle of all axes and the negative frequency terms in the second half of all axes, in order of decreasingly negative frequency.

See numpy.fft for details, definitions and conventions used.

Examples

>>> import numpy as np
>>> a = np.mgrid[:3, :3, :3][0]
>>> np.fft.fftn(a, axes=(1, 2))
array([[[ 0.+0.j,   0.+0.j,   0.+0.j], # may vary
        [ 0.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j]],
       [[ 9.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j]],
       [[18.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j],
        [ 0.+0.j,   0.+0.j,   0.+0.j]]])
>>> np.fft.fftn(a, (2, 2), axes=(0, 1))
array([[[ 2.+0.j,  2.+0.j,  2.+0.j], # may vary
        [ 0.+0.j,  0.+0.j,  0.+0.j]],
       [[-2.+0.j, -2.+0.j, -2.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j]]])

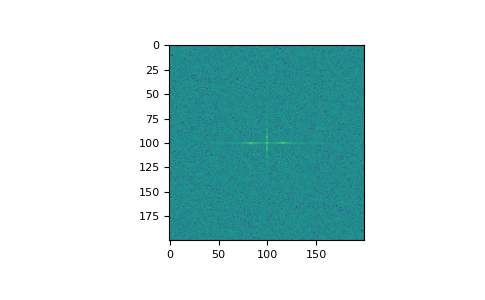
>>> import matplotlib.pyplot as plt
>>> [X, Y] = np.meshgrid(2 * np.pi * np.arange(200) / 12,
...                      2 * np.pi * np.arange(200) / 34)
>>> S = np.sin(X) + np.cos(Y) + np.random.uniform(0, 1, X.shape)
>>> FS = np.fft.fftn(S)
>>> plt.imshow(np.log(np.abs(np.fft.fftshift(FS))**2))
<matplotlib.image.AxesImage object at 0x...>
>>> plt.show()