NEP 13 — A mechanism for overriding Ufuncs

Author:

Blake Griffith

Contact:

blake.g@utexas.edu

Date:

2013-07-10

Author:

Pauli Virtanen

Author:

Nathaniel Smith

Author:

Marten van Kerkwijk

Author:

Stephan Hoyer

Date:

2017-03-31

Status:

Final

Updated:

2023-02-19

Author:

Roy Smart

Executive summary

NumPy’s universal functions (ufuncs) currently have some limited functionality for operating on user defined subclasses of ndarray using __array_prepare__ and __array_wrap__ [1], and there is little to no support for arbitrary objects. e.g. SciPy’s sparse matrices [2] [3].

Here we propose adding a mechanism to override ufuncs based on the ufunc checking each of it’s arguments for a __array_ufunc__ method. On discovery of __array_ufunc__ the ufunc will hand off the operation to the method.

This covers some of the same ground as Travis Oliphant’s proposal to retro-fit NumPy with multi-methods [4], which would solve the same problem. The mechanism here follows more closely the way Python enables classes to override __mul__ and other binary operations. It also specifically addresses how binary operators and ufuncs should interact. (Note that in earlier iterations, the override was called __numpy_ufunc__. An implementation was made, but had not quite the right behaviour, hence the change in name.)

The __array_ufunc__ as described below requires that any corresponding Python binary operations (__mul__ et al.) should be implemented in a specific way and be compatible with NumPy’s ndarray semantics. Objects that do not satisfy this cannot override any NumPy ufuncs. We do not specify a future-compatible path by which this requirement can be relaxed — any changes here require corresponding changes in 3rd party code.

[1]

http://docs.python.org/doc/numpy/user/basics.subclassing.html

[2]

scipy/scipy#2123

[3]

scipy/scipy#1569

[4]

https://technicaldiscovery.blogspot.com/2013/07/thoughts-after-scipy-2013-and-specific.html

Motivation

The current machinery for dispatching Ufuncs is generally agreed to be insufficient. There have been lengthy discussions and other proposed solutions [5], [6].

Using ufuncs with subclasses of ndarray is limited to __array_prepare__ and __array_wrap__ to prepare the output arguments, but these don’t allow you to for example change the shape or the data of the arguments. Trying to ufunc things that don’t subclass ndarray is even more difficult, as the input arguments tend to be cast to object arrays, which ends up producing surprising results.

Take this example of ufuncs interoperability with sparse matrices.:

In [1]: import numpy as np
import scipy.sparse as sp

a = np.random.randint(5, size=(3,3))
b = np.random.randint(5, size=(3,3))

asp = sp.csr_matrix(a)
bsp = sp.csr_matrix(b)

In [2]: a, b
Out[2]:(array([[0, 4, 4],
               [1, 3, 2],
               [1, 3, 1]]),
        array([[0, 1, 0],
               [0, 0, 1],
               [4, 0, 1]]))

In [3]: np.multiply(a, b) # The right answer
Out[3]: array([[0, 4, 0],
               [0, 0, 2],
               [4, 0, 1]])

In [4]: np.multiply(asp, bsp).todense() # calls __mul__ which does matrix multi
Out[4]: matrix([[16,  0,  8],
                [ 8,  1,  5],
                [ 4,  1,  4]], dtype=int64)

In [5]: np.multiply(a, bsp) # Returns NotImplemented to user, bad!
Out[5]: NotImplemented

Returning NotImplemented to user should not happen. Moreover:

In [6]: np.multiply(asp, b)
Out[6]: array([[ <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>,
                    <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>,
                    <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>],
                   [ <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>,
                    <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>,
                    <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>],
                   [ <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>,
                    <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>,
                    <3x3 sparse matrix of type '<class 'numpy.int64'>'
                with 8 stored elements in Compressed Sparse Row format>]], dtype=object)

Here, it appears that the sparse matrix was converted to an object array scalar, which was then multiplied with all elements of the b array. However, this behavior is more confusing than useful, and having a TypeError would be preferable.

This proposal will not resolve the issue with scipy.sparse matrices, which have multiplication semantics incompatible with NumPy arrays. However, the aim is to enable writing other custom array types that have strictly ndarray compatible semantics.

[5]

https://mail.python.org/pipermail/numpy-discussion/2011-June/056945.html

[6] (1,2)

numpy/numpy#5844

Proposed interface

The standard array class ndarray gains an __array_ufunc__ method and objects can override Ufuncs by overriding this method (if they are ndarray subclasses) or defining their own. The method signature is:

def __array_ufunc__(self, ufunc, method, *inputs, **kwargs)

Here:

• ufunc is the ufunc object that was called.

• method is a string indicating how the Ufunc was called, either "__call__" to indicate it was called directly, or one of its methods: "reduce", "accumulate", "reduceat", "outer", or "at".

• inputs is a tuple of the input arguments to the ufunc

• kwargs contains any optional or keyword arguments passed to the function. This includes any out arguments, which are always contained in a tuple.

Hence, the arguments are normalized: only the required input arguments (inputs) are passed on as positional arguments, all the others are passed on as a dict of keyword arguments (kwargs). In particular, if there are output arguments, positional are otherwise, that are not None, they are passed on as a tuple in the out keyword argument (even for the reduce, accumulate, and reduceat methods where in all current cases only a single output makes sense).

The function dispatch proceeds as follows:

• If one of the input, output, or where arguments implements __array_ufunc__, it is executed instead of the ufunc.

• If more than one of the arguments implements __array_ufunc__, they are tried in the following order: subclasses before superclasses, inputs before outputs, outputs before where, otherwise left to right.

• The first __array_ufunc__ method returning something else than NotImplemented determines the return value of the Ufunc.

• If all __array_ufunc__ methods of the input arguments return NotImplemented, a TypeError is raised.

• If a __array_ufunc__ method raises an error, the error is propagated immediately.

• If none of the input arguments had an __array_ufunc__ method, the execution falls back on the default ufunc behaviour.

In the above, there is one proviso: if a class has an __array_ufunc__ attribute but it is identical to ndarray.__array_ufunc__, the attribute is ignored. This happens for instances of ndarray and for ndarray subclasses that did not override their inherited __array_ufunc__ implementation.

Type casting hierarchy

The Python operator override mechanism gives much freedom in how to write the override methods, and it requires some discipline in order to achieve predictable results. Here, we discuss an approach for understanding some of the implications, which can provide input in the design.

It is useful to maintain a clear idea of what types can be “upcast” to others, possibly indirectly (e.g. indirect A->B->C is implemented but direct A->C not). If the implementations of __array_ufunc__ follow a coherent type casting hierarchy, it can be used to understand results of operations.

Type casting can be expressed as a graph defined as follows:

For each __array_ufunc__ method, draw directed edges from each possible input type to each possible output type.

That is, in each case where y = x.__array_ufunc__(a, b, c, ...) does something else than returning NotImplemented or raising an error, draw edges type(a) -> type(y), type(b) -> type(y), …

If the resulting graph is acyclic, it defines a coherent type casting hierarchy (unambiguous partial ordering between types). In this case, operations involving multiple types generally predictably produce result of the “highest” type, or raise a TypeError. See examples at the end of this section.

If the graph has cycles, the __array_ufunc__ type casting is not well-defined, and things such as type(multiply(a, b)) != type(multiply(b, a)) or type(add(a, add(b, c))) != type(add(add(a, b), c)) are not excluded (and then probably always possible).

If the type casting hierarchy is well defined, for each class A, all other classes that define __array_ufunc__ belong to exactly one of three groups:

• Above A: the types that A can be (indirectly) upcast to in ufuncs.

• Below A: the types that can be (indirectly) upcast to A in ufuncs.

• Incompatible: neither above nor below A; types for which no (indirect) upcasting is possible.

Note that the legacy behaviour of NumPy ufuncs is to try to convert unknown objects to ndarray via np.asarray(). This is equivalent to placing ndarray above these objects in the graph. Since we above defined ndarray to return NotImplemented for classes with custom __array_ufunc__, this puts ndarray below such classes in the type hierarchy, allowing the operations to be overridden.

In view of the above, binary ufuncs describing transitive operations should aim to define a well-defined casting hierarchy. This is likely also a sensible approach to all ufuncs — exceptions to this should consider carefully if any surprising behavior results.

Example

Type casting hierarchy.

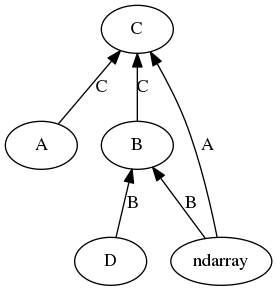
The __array_ufunc__ of type A can handle ndarrays returning C, B can handle ndarray and D returning B, and C can handle A and B returning C, but not ndarrays or D. The result is a directed acyclic graph, and defines a type casting hierarchy, with relations C > A, C > ndarray, C > B > ndarray, C > B > D. The type A is incompatible with B, D, ndarray, and D is incompatible with A and ndarray. Ufunc expressions involving these classes should produce results of the highest type involved or raise a TypeError.

Example

One-cycle in the __array_ufunc__ graph.

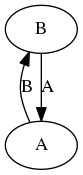
In this case, the __array_ufunc__ relations have a cycle of length 1, and a type casting hierarchy does not exist. Binary operations are not commutative: type(a + b) is A but type(b + a) is B.

Example

Longer cycle in the __array_ufunc__ graph.

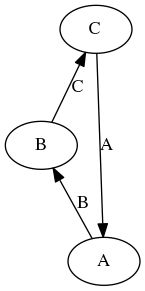
In this case, the __array_ufunc__ relations have a longer cycle, and a type casting hierarchy does not exist. Binary operations are still commutative, but type transitivity is lost: type(a + (b + c)) is A but type((a + b) + c) is C.

Subclass hierarchies

Generally, it is desirable to mirror the class hierarchy in the ufunc type casting hierarchy. The recommendation is that an __array_ufunc__ implementation of a class should generally return NotImplemented unless the inputs are instances of the same class or superclasses. This guarantees that in the type casting hierarchy, superclasses are below, subclasses above, and other classes are incompatible. Exceptions to this need to check they respect the implicit type casting hierarchy.

Note

Note that type casting hierarchy and class hierarchy are here defined to go the “opposite” directions. It would in principle also be consistent to have __array_ufunc__ handle also instances of subclasses. In this case, the “subclasses first” dispatch rule would ensure a relatively similar outcome. However, the behavior is then less explicitly specified.

Subclasses can be easily constructed if methods consistently use super() to pass through the class hierarchy [7]. To support this, ndarray has its own __array_ufunc__ method, equivalent to:

def __array_ufunc__(self, ufunc, method, *inputs, **kwargs):
    # Cannot handle items that have __array_ufunc__ (other than our own).
    outputs = kwargs.get('out', ())
    objs = inputs + outputs
    if "where" in kwargs:
        objs = objs + (kwargs["where"], )
    for item in objs:
        if (hasattr(item, '__array_ufunc__') and
                type(item).__array_ufunc__ is not ndarray.__array_ufunc__):
            return NotImplemented

    # If we didn't have to support legacy behaviour (__array_prepare__,
    # __array_wrap__, etc.), we might here convert python floats,
    # lists, etc, to arrays with
    # items = [np.asarray(item) for item in inputs]
    # and then start the right iterator for the given method.
    # However, we do have to support legacy, so call back into the ufunc.
    # Its arguments are now guaranteed not to have __array_ufunc__
    # overrides, and it will do the coercion to array for us.
    return getattr(ufunc, method)(*items, **kwargs)

Note that, as a special case, the ufunc dispatch mechanism does not call this ndarray.__array_ufunc__ method, even for ndarray subclasses if they have not overridden the default ndarray implementation. As a consequence, calling ndarray.__array_ufunc__ will not result to a nested ufunc dispatch cycle.

The use of super() should be particularly useful for subclasses of ndarray that only add an attribute like a unit. In their __array_ufunc__ implementation, such classes can do possible adjustment of the arguments relevant to their own class, and pass on to the superclass implementation using super() until the ufunc is actually done, and then do possible adjustments of the outputs.

In general, custom implementations of __array_ufunc__ should avoid nested dispatch cycles, where one not just calls the ufunc via getattr(ufunc, method)(*items, **kwargs), but catches possible exceptions, etc. As always, there may be exceptions. For instance, for a class like MaskedArray, which only cares that whatever it contains is an ndarray subclass, a reimplementation with __array_ufunc__ may well be more easily done by directly applying the ufunc to its data, and then adjusting the mask. Indeed, one can think of this as part of the class determining whether it can handle the other argument (i.e., where in the type hierarchy it sits). In this case, one should return NotImplemented if the trial fails. So, the implementation would be something like:

def __array_ufunc__(self, ufunc, method, *inputs, **kwargs):
    # for simplicity, outputs are ignored here.
    unmasked_items = tuple((item.data if isinstance(item, MaskedArray)
                            else item) for item in inputs)
    try:
        unmasked_result = getattr(ufunc, method)(*unmasked_items, **kwargs)
    except TypeError:
        return NotImplemented
    # for simplicity, ignore that unmasked_result could be a tuple
    # or a scalar.
    if not isinstance(unmasked_result, np.ndarray):
        return NotImplemented
    # now combine masks and view as MaskedArray instance
    ...

As a specific example, consider a quantity and a masked array class which both override __array_ufunc__, with specific instances q and ma, where the latter contains a regular array. Executing np.multiply(q, ma), the ufunc will first dispatch to q.__array_ufunc__, which returns NotImplemented (since the quantity class turns itself into an array and calls super(), which passes on to ndarray.__array_ufunc__, which sees the override on ma). Next, ma.__array_ufunc__ gets a chance. It does not know quantity, and if it were to just return NotImplemented as well, an TypeError would result. But in our sample implementation, it uses getattr(ufunc, method) to, effectively, evaluate np.multiply(q, ma.data). This again will pass to q.__array_ufunc__, but this time, since ma.data is a regular array, it will return a result that is also a quantity. Since this is a subclass of ndarray, ma.__array_ufunc__ can turn this into a masked array and thus return a result (obviously, if it was not a array subclass, it could still return NotImplemented).

Note that in the context of the type hierarchy discussed above this is a somewhat tricky example, since MaskedArray has a strange position: it is above all subclasses of ndarray, in that it can cast them to its own type, but it does not itself know how to interact with them in ufuncs.

[7]

https://rhettinger.wordpress.com/2011/05/26/super-considered-super/

Turning Ufuncs off

For some classes, Ufuncs make no sense, and, like for some other special methods such as __hash__ and __iter__ [8], one can indicate Ufuncs are not available by setting __array_ufunc__ to None. If a Ufunc is called on any operand that sets __array_ufunc__ = None, it will unconditionally raise TypeError.

In the type casting hierarchy, this makes it explicit that the type is incompatible relative to ndarray.

[8]

https://docs.python.org/3/reference/datamodel.html#specialnames

Behavior in combination with Python’s binary operations

The Python operator override mechanism in ndarray is coupled to the __array_ufunc__ mechanism. For the special methods calls such as ndarray.__mul__(self, other) that Python calls for implementing binary operations such as * and +, NumPy’s ndarray implements the following behavior:

• If other.__array_ufunc__ is None, ndarray returns NotImplemented. Control reverts to Python, which in turn will try calling a corresponding reflexive method on other (e.g., other.__rmul__), if present.

• If the __array_ufunc__ attribute is absent on other and other.__array_priority__ > self.__array_priority__, ndarray also returns NotImplemented (and the logic proceeds as in the previous case). This ensures backwards compatibility with old versions of NumPy.

• Otherwise, ndarray unilaterally calls the corresponding Ufunc. Ufuncs never return NotImplemented, so reflexive methods such as other.__rmul__ cannot be used to override arithmetic with NumPy arrays if __array_ufunc__ is set to any value other than None. Instead, their behavior needs to be changed by implementing __array_ufunc__ in a fashion consistent with the corresponding Ufunc, e.g., np.multiply. See List of operators and NumPy Ufuncs for a list of affected operators and their corresponding ufuncs.

A class wishing to modify the interaction with ndarray in binary operations therefore has two options:

1. Implement __array_ufunc__ and follow NumPy semantics for Python binary operations (see below).

2. Set __array_ufunc__ = None, and implement Python binary operations freely. In this case, ufuncs called on this argument will raise TypeError (see Turning Ufuncs off).

Recommendations for implementing binary operations

For most numerical classes, the easiest way to override binary operations is thus to define __array_ufunc__ and override the corresponding Ufunc. The class can then, like ndarray itself, define the binary operators in terms of Ufuncs. Here, one has to take some care to ensure that one allows for other classes to indicate they are not compatible, i.e., implementations should be something like:

def _disables_array_ufunc(obj):
    try:
        return obj.__array_ufunc__ is None
    except AttributeError:
        return False

class ArrayLike:
    ...
    def __array_ufunc__(self, ufunc, method, *inputs, **kwargs):
        ...
        return result

    # Option 1: call ufunc directly
    def __mul__(self, other):
        if _disables_array_ufunc(other):
            return NotImplemented
        return np.multiply(self, other)

    def __rmul__(self, other):
        if _disables_array_ufunc(other):
            return NotImplemented
        return np.multiply(other, self)

    def __imul__(self, other):
        return np.multiply(self, other, out=(self,))

    # Option 2: call into one's own __array_ufunc__
    def __mul__(self, other):
        return self.__array_ufunc__(np.multiply, '__call__', self, other)

    def __rmul__(self, other):
        return self.__array_ufunc__(np.multiply, '__call__', other, self)

    def __imul__(self, other):
        result = self.__array_ufunc__(np.multiply, '__call__', self, other,
                                      out=(self,))
        if result is NotImplemented:
            raise TypeError(...)

To see why some care is necessary, consider another class other that does not know how to deal with arrays and ufuncs, and thus has set __array_ufunc__ to None, but does know how to do multiplication:

class MyObject:
    __array_ufunc__ = None
    def __init__(self, value):
        self.value = value
    def __repr__(self):
        return "MyObject({!r})".format(self.value)
    def __mul__(self, other):
        return MyObject(1234)
    def __rmul__(self, other):
        return MyObject(4321)

For either option above, we get the expected result:

mine = MyObject(0)
arr = ArrayLike([0])

mine * arr    # -> MyObject(1234)
mine *= arr   # -> MyObject(1234)
arr * mine    # -> MyObject(4321)
arr *= mine   # -> TypeError

Here, in the first and second example, mine.__mul__(arr) gets called and the result arrives immediately. In the third example, first arr.__mul__(mine) is called. In option (1), the check on mine.__array_ufunc__ is None will succeed and thus NotImplemented is returned, which causes mine.__rmul__(arg) to be executed. In option (2), it is presumably inside arr.__array_ufunc__ that it becomes clear that the other argument cannot be dealt with, and again NotImplemented is returned, causing control to pass to mine.__rmul__.

For the fourth example, with the in-place operators, we have here followed ndarray and ensure we never return NotImplemented, but rather raise a TypeError. In option (1) this happens indirectly: we pass to np.multiply, which in turn immediately raises TypeError, because one of its operands (out[0]) disables Ufuncs. In option (2), we pass directly to arr.__array_ufunc__, which will return NotImplemented, which we catch.

Note

the reason for not allowing in-place operations to return NotImplemented is that these cannot generically be replaced by a simple reverse operation: most array operations assume the contents of the instance are changed in-place, and do not expect a new instance. Also, what would ndarr[:] *= mine imply? Assuming it means ndarr[:] = ndarr[:] * mine, as python does by default if the ndarr.__imul__ were to return NotImplemented, is likely to be wrong.

Now consider what would happen if we had not added checks. For option (1), the relevant case is if we had not checked whether __array_func__ was set to None. In the third example, arr.__mul__(mine) is called, and without the check, this would go to np.multiply(arr, mine). This tries arr.__array_ufunc__, which returns NotImplemented and sees that mine.__array_ufunc__ is None, so a TypeError is raised.

For option (2), the relevant example is the fourth, with arr *= mine: if we had let the NotImplemented pass, python would have replaced this with arr = mine.__rmul__(arr), which is not wanted.

Because the semantics of Ufunc overrides and Python’s binary operations are nearly identical, in most cases options (1) and (2) will yield the same result with the same implementation of __array_ufunc__. One exception is the order in which implementations are tried when the second argument is a subclass of the first argument, due to a Python bug [9] expected to be fixed in Python 3.7.

In general, we recommend adopting option (1), which is the option most similar to that used by ndarray itself. Note that option (1) is viral, in the sense that any other class that wishes to support binary operations with your class now must also follow these rules for supporting binary arithmetic with ndarray (i.e., they must either implement __array_ufunc__ or set it to None). We believe this is a good thing, because it ensures the consistency of ufuncs and arithmetic on all objects that support them.

To make implementing such array-like classes easier, the mixin class NDArrayOperatorsMixin provides option (1) style overrides for all binary operators with corresponding Ufuncs. Classes that wish to implement __array_ufunc__ for compatible versions of NumPy but that also need to support binary arithmetic with NumPy arrays on older versions should ensure that __array_ufunc__ can also be used to implement all binary operations they support.

Finally, we note that we had extensive discussion about whether it might make more sense to ask classes like MyObject to implement a full __array_ufunc__ [6]. In the end, allowing classes to opt out was preferred, and the above reasoning led us to agree on a similar implementation for ndarray itself. The opt-out mechanism requires disabling Ufuncs so a class cannot define a Ufuncs to return a different result than the corresponding binary operations (i.e., if np.add(x, y) is defined, it should match x + y). Our goal was to simplify the dispatch logic for binary operations with NumPy arrays as much as possible, by making it possible to use Python’s dispatch rules or NumPy’s dispatch rules, but not some mixture of both at the same time.

[9]

https://bugs.python.org/issue30140

List of operators and NumPy Ufuncs

Here is a full list of Python binary operators and the corresponding NumPy Ufuncs used by ndarray and NDArrayOperatorsMixin:

Symbol	Operator	NumPy Ufunc(s)
<	lt	less()
<=	le	less_equal()
==	eq	equal()
!=	ne	not_equal()
>	gt	greater()
>=	ge	greater_equal()
+	add	add()
-	sub	subtract()
*	mul	multiply()
/	truediv (Python 3)	true_divide()
/	div (Python 2)	divide()
//	floordiv	floor_divide()
%	mod	remainder()
NA	divmod	divmod()
**	pow	power() [10]
<<	lshift	left_shift()
>>	rshift	right_shift()
&	and_	bitwise_and()
^	xor_	bitwise_xor()
|	or_	bitwise_or()
@	matmul	Not yet implemented as a ufunc [11]

And here is the list of unary operators:

Symbol	Operator	NumPy Ufunc(s)
-	neg	negative()
+	pos	positive() [12]
NA	abs	absolute()
~	invert	invert()

[10]

class :ndarray takes short cuts for __pow__ for the cases where the power equals 1 (positive()), -1 (reciprocal()), 2 (square()), 0 (an otherwise private _ones_like ufunc), and 0.5 (sqrt()), and the array is float or complex (or integer for square).

[11]

Because NumPy’s matmul() is not a ufunc, it is currently not possible to override numpy_array @ other with other taking precedence if other implements __array_func__.

[12]

ndarray currently does a copy instead of using this ufunc.

Future extensions to other functions

Some NumPy functions could be implemented as (generalized) Ufunc, in which case it would be possible for them to be overridden by the __array_ufunc__ method. A prime candidate is matmul(), which currently is not a Ufunc, but could be relatively easily be rewritten as a (set of) generalized Ufuncs. The same may happen with functions such as median(), min(), and argsort().