numpy.random.Generator.geometric#
method
- random.Generator.geometric(p, size=None)#
Draw samples from the geometric distribution.
Bernoulli trials are experiments with one of two outcomes: success or failure (an example of such an experiment is flipping a coin). The geometric distribution models the number of trials that must be run in order to achieve success. It is therefore supported on the positive integers,
k = 1, 2, ....The probability mass function of the geometric distribution is
\[f(k) = (1 - p)^{k - 1} p\]where p is the probability of success of an individual trial.
- Parameters:
- pfloat or array_like of floats
The probability of success of an individual trial.
- sizeint or tuple of ints, optional
Output shape. If the given shape is, e.g.,
(m, n, k), thenm * n * ksamples are drawn. If size isNone(default), a single value is returned ifpis a scalar. Otherwise,np.array(p).sizesamples are drawn.
- Returns:
- outndarray or scalar
Drawn samples from the parameterized geometric distribution.
References
[1]Wikipedia, “Geometric distribution”, https://en.wikipedia.org/wiki/Geometric_distribution
Examples
Draw 10,000 values from the geometric distribution, with the probability of an individual success equal to
p = 0.35:>>> p, size = 0.35, 10000 >>> rng = np.random.default_rng() >>> sample = rng.geometric(p=p, size=size)
What proportion of trials succeeded after a single run?
>>> (sample == 1).sum()/size 0.34889999999999999 # may vary
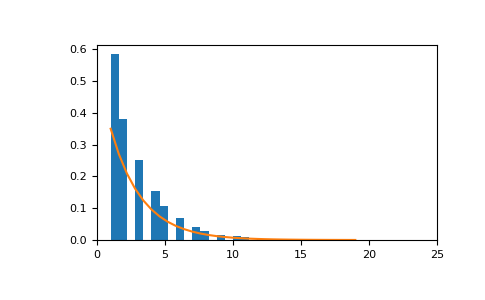
The geometric distribution with
p=0.35looks as follows:>>> import matplotlib.pyplot as plt >>> count, bins, _ = plt.hist(sample, bins=30, density=True) >>> plt.plot(bins, (1-p)**(bins-1)*p) >>> plt.xlim([0, 25]) >>> plt.show()