numpy.random.Generator.multivariate_normal

method

random.Generator.multivariate_normal(mean, cov, size=None, check_valid='warn', tol=1e-8, *, method='svd')

Draw random samples from a multivariate normal distribution.

The multivariate normal, multinormal or Gaussian distribution is a generalization of the one-dimensional normal distribution to higher dimensions. Such a distribution is specified by its mean and covariance matrix. These parameters are analogous to the mean (average or “center”) and variance (standard deviation, or “width,” squared) of the one-dimensional normal distribution.

Parameters

mean1-D array_like, of length N

Mean of the N-dimensional distribution.

cov2-D array_like, of shape (N, N)

Covariance matrix of the distribution. It must be symmetric and positive-semidefinite for proper sampling.

sizeint or tuple of ints, optional

Given a shape of, for example, (m,n,k), m*n*k samples are generated, and packed in an m-by-n-by-k arrangement. Because each sample is N-dimensional, the output shape is (m,n,k,N). If no shape is specified, a single (N-D) sample is returned.

check_valid{ ‘warn’, ‘raise’, ‘ignore’ }, optional

Behavior when the covariance matrix is not positive semidefinite.

tolfloat, optional

Tolerance when checking the singular values in covariance matrix. cov is cast to double before the check.

method{ ‘svd’, ‘eigh’, ‘cholesky’}, optional

The cov input is used to compute a factor matrix A such that A @ A.T = cov. This argument is used to select the method used to compute the factor matrix A. The default method ‘svd’ is the slowest, while ‘cholesky’ is the fastest but less robust than the slowest method. The method eigh uses eigen decomposition to compute A and is faster than svd but slower than cholesky.

New in version 1.18.0.

Returns

outndarray

The drawn samples, of shape size, if that was provided. If not, the shape is (N,).

In other words, each entry out[i,j,...,:] is an N-dimensional value drawn from the distribution.

Notes

The mean is a coordinate in N-dimensional space, which represents the location where samples are most likely to be generated. This is analogous to the peak of the bell curve for the one-dimensional or univariate normal distribution.

Covariance indicates the level to which two variables vary together. From the multivariate normal distribution, we draw N-dimensional samples, \(X = [x_1, x_2, ... x_N]\). The covariance matrix element \(C_{ij}\) is the covariance of \(x_i\) and \(x_j\). The element \(C_{ii}\) is the variance of \(x_i\) (i.e. its “spread”).

Instead of specifying the full covariance matrix, popular approximations include:

• Spherical covariance (cov is a multiple of the identity matrix)

• Diagonal covariance (cov has non-negative elements, and only on the diagonal)

This geometrical property can be seen in two dimensions by plotting generated data-points:

>>> mean = [0, 0]
>>> cov = [[1, 0], [0, 100]]  # diagonal covariance

Diagonal covariance means that points are oriented along x or y-axis:

>>> import matplotlib.pyplot as plt
>>> x, y = np.random.default_rng().multivariate_normal(mean, cov, 5000).T
>>> plt.plot(x, y, 'x')
>>> plt.axis('equal')
>>> plt.show()

Note that the covariance matrix must be positive semidefinite (a.k.a. nonnegative-definite). Otherwise, the behavior of this method is undefined and backwards compatibility is not guaranteed.

References

1

Papoulis, A., “Probability, Random Variables, and Stochastic Processes,” 3rd ed., New York: McGraw-Hill, 1991.

2

Duda, R. O., Hart, P. E., and Stork, D. G., “Pattern Classification,” 2nd ed., New York: Wiley, 2001.

Examples

>>> mean = (1, 2)
>>> cov = [[1, 0], [0, 1]]
>>> rng = np.random.default_rng()
>>> x = rng.multivariate_normal(mean, cov, (3, 3))
>>> x.shape
(3, 3, 2)

We can use a different method other than the default to factorize cov:

>>> y = rng.multivariate_normal(mean, cov, (3, 3), method='cholesky')
>>> y.shape
(3, 3, 2)

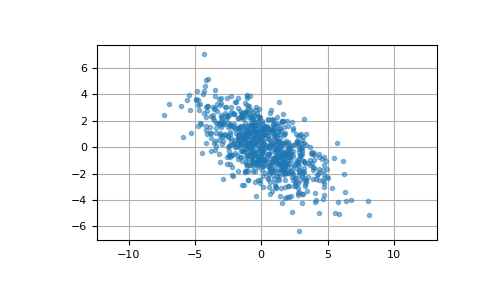
Here we generate 800 samples from the bivariate normal distribution with mean [0, 0] and covariance matrix [[6, -3], [-3, 3.5]]. The expected variances of the first and second components of the sample are 6 and 3.5, respectively, and the expected correlation coefficient is -3/sqrt(6*3.5) ≈ -0.65465.

>>> cov = np.array([[6, -3], [-3, 3.5]])
>>> pts = rng.multivariate_normal([0, 0], cov, size=800)

Check that the mean, covariance, and correlation coefficient of the sample are close to the expected values:

>>> pts.mean(axis=0)
array([ 0.0326911 , -0.01280782])  # may vary
>>> np.cov(pts.T)
array([[ 5.96202397, -2.85602287],
       [-2.85602287,  3.47613949]])  # may vary
>>> np.corrcoef(pts.T)[0, 1]
-0.6273591314603949  # may vary

We can visualize this data with a scatter plot. The orientation of the point cloud illustrates the negative correlation of the components of this sample.

>>> import matplotlib.pyplot as plt
>>> plt.plot(pts[:, 0], pts[:, 1], '.', alpha=0.5)
>>> plt.axis('equal')
>>> plt.grid()
>>> plt.show()

previous

numpy.random.Generator.multivariate_hypergeometric

next

numpy.random.Generator.negative_binomial