numpy.random.RandomState.vonmises

method

random.RandomState.vonmises(mu, kappa, size=None)

Draw samples from a von Mises distribution.

Samples are drawn from a von Mises distribution with specified mode (mu) and dispersion (kappa), on the interval [-pi, pi].

The von Mises distribution (also known as the circular normal distribution) is a continuous probability distribution on the unit circle. It may be thought of as the circular analogue of the normal distribution.

Note

New code should use the vonmises method of a Generator instance instead; please see the Quick Start.

Parameters:

mufloat or array_like of floats

Mode (“center”) of the distribution.

kappafloat or array_like of floats

Dispersion of the distribution, has to be >=0.

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. If size is None (default), a single value is returned if mu and kappa are both scalars. Otherwise, np.broadcast(mu, kappa).size samples are drawn.

Returns:

outndarray or scalar

Drawn samples from the parameterized von Mises distribution.

See also

scipy.stats.vonmises

probability density function, distribution, or cumulative density function, etc.

random.Generator.vonmises

which should be used for new code.

Notes

The probability density for the von Mises distribution is

\[p(x) = \frac{e^{\kappa cos(x-\mu)}}{2\pi I_0(\kappa)},\]

where \(\mu\) is the mode and \(\kappa\) the dispersion, and \(I_0(\kappa)\) is the modified Bessel function of order 0.

The von Mises is named for Richard Edler von Mises, who was born in Austria-Hungary, in what is now the Ukraine. He fled to the United States in 1939 and became a professor at Harvard. He worked in probability theory, aerodynamics, fluid mechanics, and philosophy of science.

References

[1]

Abramowitz, M. and Stegun, I. A. (Eds.). “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing,” New York: Dover, 1972.

[2]

von Mises, R., “Mathematical Theory of Probability and Statistics”, New York: Academic Press, 1964.

Examples

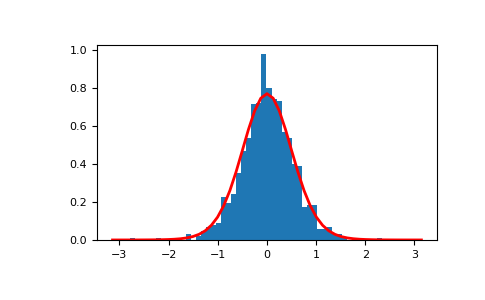
Draw samples from the distribution:

>>> mu, kappa = 0.0, 4.0 # mean and dispersion
>>> s = np.random.vonmises(mu, kappa, 1000)

Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> from scipy.special import i0  
>>> plt.hist(s, 50, density=True)
>>> x = np.linspace(-np.pi, np.pi, num=51)
>>> y = np.exp(kappa*np.cos(x-mu))/(2*np.pi*i0(kappa))  
>>> plt.plot(x, y, linewidth=2, color='r')  
>>> plt.show()