numpy.random.dirichlet

random.dirichlet(alpha, size=None)

Draw samples from the Dirichlet distribution.

Draw size samples of dimension k from a Dirichlet distribution. A Dirichlet-distributed random variable can be seen as a multivariate generalization of a Beta distribution. The Dirichlet distribution is a conjugate prior of a multinomial distribution in Bayesian inference.

Note

New code should use the dirichlet method of a Generator instance instead; please see the Quick Start.

Parameters:

alphasequence of floats, length k

Parameter of the distribution (length k for sample of length k).

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n), then m * n * k samples are drawn. Default is None, in which case a vector of length k is returned.

Returns:

samplesndarray,

The drawn samples, of shape (size, k).

Raises:

ValueError

If any value in alpha is less than or equal to zero

See also

random.Generator.dirichlet

which should be used for new code.

Notes

The Dirichlet distribution is a distribution over vectors \(x\) that fulfil the conditions \(x_i>0\) and \(\sum_{i=1}^k x_i = 1\).

The probability density function \(p\) of a Dirichlet-distributed random vector \(X\) is proportional to

\[p(x) \propto \prod_{i=1}^{k}{x^{\alpha_i-1}_i},\]

where \(\alpha\) is a vector containing the positive concentration parameters.

The method uses the following property for computation: let \(Y\) be a random vector which has components that follow a standard gamma distribution, then \(X = \frac{1}{\sum_{i=1}^k{Y_i}} Y\) is Dirichlet-distributed

References

[1]

David McKay, “Information Theory, Inference and Learning Algorithms,” chapter 23, http://www.inference.org.uk/mackay/itila/

[2]

Wikipedia, “Dirichlet distribution”, https://en.wikipedia.org/wiki/Dirichlet_distribution

Examples

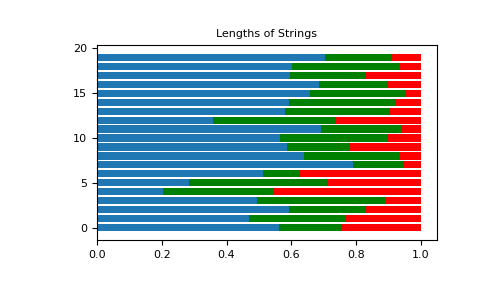
Taking an example cited in Wikipedia, this distribution can be used if one wanted to cut strings (each of initial length 1.0) into K pieces with different lengths, where each piece had, on average, a designated average length, but allowing some variation in the relative sizes of the pieces.

>>> s = np.random.dirichlet((10, 5, 3), 20).transpose()

>>> import matplotlib.pyplot as plt
>>> plt.barh(range(20), s[0])
>>> plt.barh(range(20), s[1], left=s[0], color='g')
>>> plt.barh(range(20), s[2], left=s[0]+s[1], color='r')
>>> plt.title("Lengths of Strings")