numpy.random.Generator.chisquare#
method
- random.Generator.chisquare(df, size=None)#
Draw samples from a chi-square distribution.
When df independent random variables, each with standard normal distributions (mean 0, variance 1), are squared and summed, the resulting distribution is chi-square (see Notes). This distribution is often used in hypothesis testing.
- Parameters:
- dffloat or array_like of floats
Number of degrees of freedom, must be > 0.
- sizeint or tuple of ints, optional
Output shape. If the given shape is, e.g.,
(m, n, k), thenm * n * ksamples are drawn. If size isNone(default), a single value is returned ifdfis a scalar. Otherwise,np.array(df).sizesamples are drawn.
- Returns:
- outndarray or scalar
Drawn samples from the parameterized chi-square distribution.
- Raises:
- ValueError
When df <= 0 or when an inappropriate
size(e.g.size=-1) is given.
Notes
The variable obtained by summing the squares of df independent, standard normally distributed random variables:
\[Q = \sum_{i=1}^{\mathtt{df}} X^2_i\]is chi-square distributed, denoted
\[Q \sim \chi^2_k.\]The probability density function of the chi-squared distribution is
\[p(x) = \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2},\]where \(\Gamma\) is the gamma function,
\[\Gamma(x) = \int_0^{-\infty} t^{x - 1} e^{-t} dt.\]References
[1]NIST “Engineering Statistics Handbook” https://www.itl.nist.gov/div898/handbook/eda/section3/eda3666.htm
Examples
>>> rng = np.random.default_rng() >>> rng.chisquare(2,4) array([ 1.89920014, 9.00867716, 3.13710533, 5.62318272]) # random
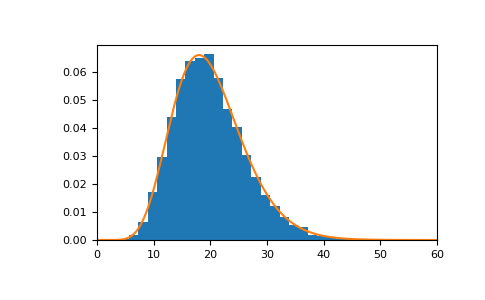
The distribution of a chi-square random variable with 20 degrees of freedom looks as follows:
>>> import matplotlib.pyplot as plt >>> import scipy.stats as stats >>> s = rng.chisquare(20, 10000) >>> count, bins, _ = plt.hist(s, 30, density=True) >>> x = np.linspace(0, 60, 1000) >>> plt.plot(x, stats.chi2.pdf(x, df=20)) >>> plt.xlim([0, 60]) >>> plt.show()