numpy.random.Generator.pareto

method

random.Generator.pareto(a, size=None)

Draw samples from a Pareto II (AKA Lomax) distribution with specified shape.

Parameters:

afloat or array_like of floats

Shape of the distribution. Must be positive.

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. If size is None (default), a single value is returned if a is a scalar. Otherwise, np.array(a).size samples are drawn.

Returns:

outndarray or scalar

Drawn samples from the Pareto II distribution.

See also

scipy.stats.pareto

Pareto I distribution

scipy.stats.lomax

Lomax (Pareto II) distribution

scipy.stats.genpareto

Generalized Pareto distribution

Notes

The probability density for the Pareto II distribution is

\[p(x) = \frac{a}{{x+1}^{a+1}} , x \ge 0\]

where \(a > 0\) is the shape.

The Pareto II distribution is a shifted and scaled version of the Pareto I distribution, which can be found in scipy.stats.pareto.

References

[1]

Francis Hunt and Paul Johnson, On the Pareto Distribution of Sourceforge projects.

[2]

Pareto, V. (1896). Course of Political Economy. Lausanne.

[3]

Reiss, R.D., Thomas, M.(2001), Statistical Analysis of Extreme Values, Birkhauser Verlag, Basel, pp 23-30.

[4]

Wikipedia, “Pareto distribution”, https://en.wikipedia.org/wiki/Pareto_distribution

Examples

Draw samples from the distribution:

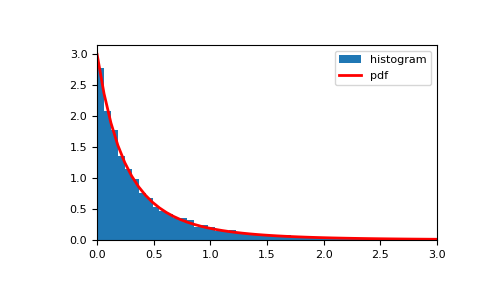
>>> a = 3.
>>> rng = np.random.default_rng()
>>> s = rng.pareto(a, 10000)

Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 3, 50)
>>> pdf = a / (x+1)**(a+1)
>>> plt.hist(s, bins=x, density=True, label='histogram')
>>> plt.plot(x, pdf, linewidth=2, color='r', label='pdf')
>>> plt.xlim(x.min(), x.max())
>>> plt.legend()
>>> plt.show()