numpy.random.Generator.exponential

method

random.Generator.exponential(scale=1.0, size=None)

Draw samples from an exponential distribution.

Its probability density function is

\[f(x; \frac{1}{\beta}) = \frac{1}{\beta} \exp(-\frac{x}{\beta}),\]

for x > 0 and 0 elsewhere. \(\beta\) is the scale parameter, which is the inverse of the rate parameter \(\lambda = 1/\beta\). The rate parameter is an alternative, widely used parameterization of the exponential distribution [3].

The exponential distribution is a continuous analogue of the geometric distribution. It describes many common situations, such as the size of raindrops measured over many rainstorms [1], or the time between page requests to Wikipedia [2].

Parameters:

scalefloat or array_like of floats

The scale parameter, \(\beta = 1/\lambda\). Must be non-negative.

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn. If size is None (default), a single value is returned if scale is a scalar. Otherwise, np.array(scale).size samples are drawn.

Returns:

outndarray or scalar

Drawn samples from the parameterized exponential distribution.

References

[1]

Peyton Z. Peebles Jr., “Probability, Random Variables and Random Signal Principles”, 4th ed, 2001, p. 57.

[2]

Wikipedia, “Poisson process”, https://en.wikipedia.org/wiki/Poisson_process

[3]

Wikipedia, “Exponential distribution”, https://en.wikipedia.org/wiki/Exponential_distribution

Examples

Assume a company has 10000 customer support agents and the time between customer calls is exponentially distributed and that the average time between customer calls is 4 minutes.

>>> scale, size = 4, 10000
>>> rng = np.random.default_rng()
>>> time_between_calls = rng.exponential(scale=scale, size=size)

What is the probability that a customer will call in the next 4 to 5 minutes?

>>> x = ((time_between_calls < 5).sum())/size
>>> y = ((time_between_calls < 4).sum())/size
>>> x - y
0.08  # may vary

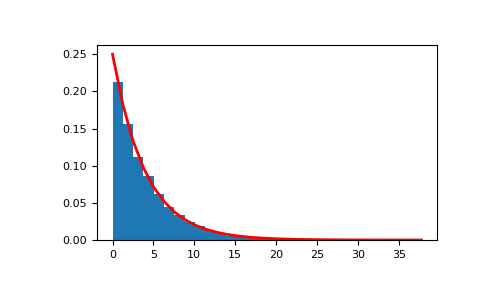
The corresponding distribution can be visualized as follows:

>>> import matplotlib.pyplot as plt
>>> scale, size = 4, 10000
>>> rng = np.random.default_rng()
>>> sample = rng.exponential(scale=scale, size=size)
>>> count, bins, _ = plt.hist(sample, 30, density=True)
>>> plt.plot(bins, scale**(-1)*np.exp(-scale**-1*bins), linewidth=2, color='r')
>>> plt.show()